#002 - Generation

Overview

When I first conceptualized Beaconfall and it's predecessor prototype, it became pretty apparent that the heart of the game would be in it's world. While the current state of the world is quite barren, I've attempted to design the systems responsible for putting it here so that I can continue to update and bring more life to it.

This post and the next will cover the "world loop" - which is the system responsible for generating and updating the world as the player traverses through it, how it all works, the terrain generation itself, and future plans I have for it.

Generation

I think it's appropriate to start with the core of the world generation, that is, the terrain generation function.

The function takes in two parameters: a point in 3D space p, and a seed value s, and produces the distance from the surface of the terrain at point p. In discussions around open-world and especially sandbox games, the term "infinite generation" gets thrown around a lot. What that really means is that every point in 3D space can produce a valid result with this function, provided that point in 3D space can even be represented by a computer in the first place. The terrain generation function I'm using is effectively infinite by that definition.

The terrain generation function is, in truth, a form of gradient noise.

Gradient noise generated using GIMP.

Gradient noise is, simply, a smoothing of random values. Different types of gradient noise exist and are used in different applications, from terrain generation to texture generation. I implemented my own form of gradient noise that I've used in this project, which essentially uses just an infinite grid of random values and interpolates between them.

The image above is a 2D representation of gradient noise, where values between 0 and 1 are generated for each pixel on the 2D canvas. The higher the value is, the lighter the pixel is, and vice versa.

The generator responsible for the above image could already be used for simple "heightmap" terrain - where the value of each sample determines the height of the terrain at a given point.

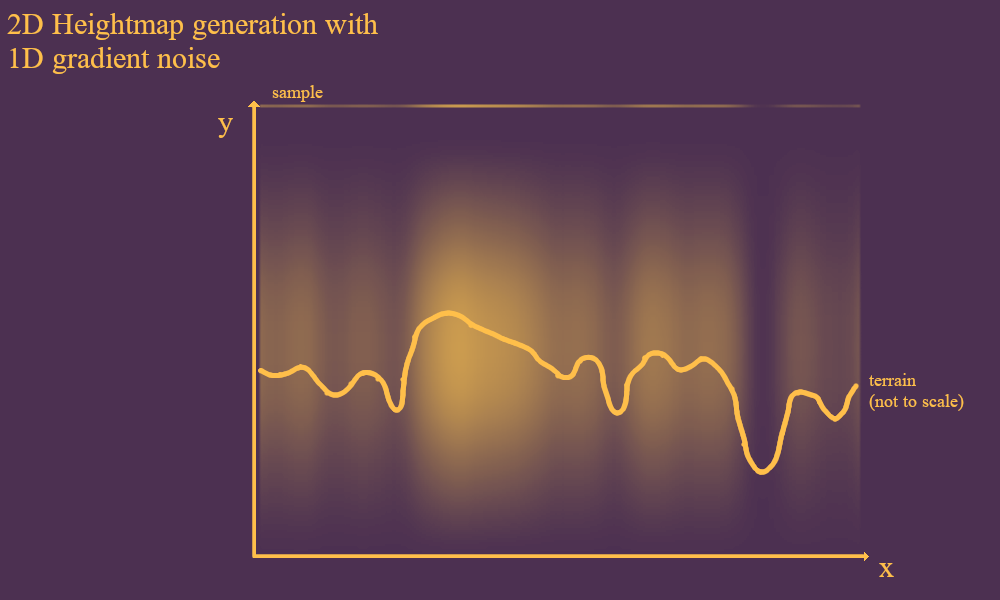
But I think we can do better than this. Heightmap terrain is simple, and due to it predicting one of the dimensions of the space it's being used for, can also be quite fast. But, it's also quite boring, in my humble opinion.

Heightmap terrain doesn't let you create any truly 3D (or, for the above example, 2D) features, like overhangs and caves. The terrain can only go in two directions: up or down, and cannot fold in on itself in interesting ways. So, for Beaconfall, I'm using a different approach.

Now, if you're reading this having played Beaconfall in it's current state (0.1, or 0.1.1), you'll note that despite my distaste for this "only up or down" approach, that sounds an awful lot like how the Beaconfall terrain generation currently works in-game.

While Beaconfall doesn't use heightmap terrain, and you can rarely encounter small overhangs and cliffs, the nature of the current generation algorithm produces terrain that looks quite a lot like your standard run-of-the-mill heightmap terrain. What's here right now is meant to serve more as a baseline for future additions, which I'll ramble about at the end of the next post.

So, in short, I'm working on it.

So, Beaconfall's terrain generation does in fact use 3D gradient noise and isn't just a 2D heightmap, but if that's all there was to it, then we'd end up with something like this:

Bearing in mind that this is a side profile (from the XY plane), that really doesn't look like typical terrain. To address this, we apply a gradient along the Y-axis.

Much better. Beaconfall uses a much sharper gradient than this, so the terrain feels much more flat and less curvaceous than this. Part of this is by design, as I want the great big mountains in this game to feel realistic. But as I continue to work on this game I might change that design philosophy.

Just for fun, let's have a look at what this game's terrain generation looks like with a wider gradient.

Welp, looks like this just broke the lighting system. Not that it matters too much, as the current system is basically just a placeholder anyway.

But hey, look, we got an overhang! An odd looking one, sure, but an overhang nonetheless.

In case you're wondering if the large mountains you see in the distance look meaningfully different, they don't. The wide mountains generated with Beaconfall are actually a separate layer of world generation in and of themselves, made with... uh... heightmap terrain, so increasing the gradient there wouldn't do much more than raise the height of these mountains.

Kinda hard to tell when they're already so far away, eh? They're 5x taller here.

One important thing to remember is that all I've described so far is the actual mathematical function used to generate the terrain. All it does is spit out a number based on a position and seed value. If that number is at or above 0, then that point is considered to be inside of the terrain. If the point is below 0, then it's outside of the terrain.

...or is it the other way around? I can't remember.

Anyways, it really doesn't matter, since this means that where the points meet 0 will determine where the surface of the terrain is, and this surface is what the meshes for the terrain need to be. So how do we get these meshes?

Sectors

Sectors are the individual building blocks of the world loop, representing subsets of the infinite terrain - analogous to chunks from Minecraft. Sectors have two primary attributes which determine how they'll generate and look: position, and scale. These two features will determine which parts of the terrain are 'applied' to these sectors during generation, as well as where they'll ultimately be drawn in the world.

Best shot I could get of a single sector.

Aside from creation and deletion, there are two main operations that the world loop will perform on each sector (bearing in mind that drawing isn't part of the world loop): sample generation, and mesh generation.

Each sector generates a set of NxNxN samples (N = SECTOR_SIZE + 1, currently SECTOR_SIZE = 32) by sampling the terrain generation function at each of those points, and recording their value at that respective location. That's sample generation, and it's pretty simple once you have the terrain function. However, due to the complexity of the terrain function, it's also the slowest part of the generation process.

In the game's first release, v0.1, cell generation would occur uniformly across all sectors, however, in v0.1.1, the number of sectors that the world loop needed to undertake increased from 270 to 1,250, due to the increase in size of each sector layer (we'll get to that next post, don't worry), and world generation became far slower as a result. To address this, cell generation now implements an "empty check" - the generation starts by sampling every Nth point, and if every point is above or below the surface of the terrain, the sector is marked as "empty" and actual generation for that sector is skipped.

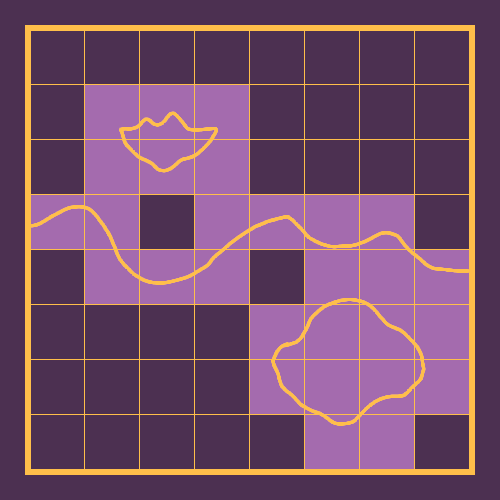
This diagram demonstrates the effect of the "empty checker" - only the highlighted sectors, where the surface is visible, are actually generated.

Once cell generation is complete, the world loop moves on to mesh generation. The algorithm I use for mesh generation is marching tetrahedra. Marching tetrahedra is the less popular younger sibling to marching cubes, however it's the same general idea. In marching cubes, you form a "box" or "cell" where each corner is a sample, and pick from a list of possible vertex/face combinations to add to the mesh at the cell, based on whether each sample is above or below the surface of the terrain.

This is marching cubes' 2D equivalent: marching squares. Marching squares has a total of 16 possible cases, while marching cubes has 256, so that's why I chose to make a diagram of this rather than marching cubes.

Marching tetrahedra is the same idea, but each cell is broken down further into 6 separate tetrahedra.

image from Wikipedia.

Since each tetrahedra only has 4 vertices, meaning 2^4=16 possible cases, this algorithm is far simpler to implement.

And, yes, I'm aware of that famous piece of code that everyone likes to copy and paste in their implementations of marching cubes, but I can almost never get it to work with my projects, and the one time it did, it was incredibly slow.

Marching tetrahedra also answers a few ambiguities found in the marching cubes algorithm, though how they're answered depends on how the tetrahedra are laid out within each cell. Since each cell (or tetrahedron) has a collection of specific values representing their distance from the surface, each vertex can be interpolated and projected to where this "zero point" might be along the edge of each tetrahedra, giving us smoothed out meshes for each sector.

And that about wraps up how individual sectors work. There's just one last thing to cover now, and that is the world itself. 

Originally, I was going to write this part out too, but just this alone has taken 6 hours out of me, between making diagrams and rewriting the same paragraph over and over again, so I think I'll call it here. I'll finish this discussion out some time this weekend where I cover the actual world loop, as well as future plans I have for the generator. Thanks for reading, and stay tuned.

- 0de